این مقاله انگلیسی ISI در نشریه Citeseerx در 20 صفحه در سال 2000 منتشر شده و ترجمه آن 22 صفحه میباشد. کیفیت ترجمه این مقاله ویژه – طلایی ⭐️⭐️⭐️ بوده و به صورت کامل ترجمه شده است.
| دانلود رایگان مقاله انگلیسی + خرید ترجمه فارسی | |
| عنوان فارسی مقاله: |
دستهبندی کدهای MDS دو و سهبعدی برای 4 ≤ q ≤ 32 |
| عنوان انگلیسی مقاله: |
Classification of 2 and 3 dimensional MDS codes for 4 ≤ q ≤ 32 |
|
|
|
| مشخصات مقاله انگلیسی | |
| فرمت مقاله انگلیسی | pdf و ورد تایپ شده با قابلیت ویرایش |
| سال انتشار | 2000 |
| تعداد صفحات مقاله انگلیسی | 20 صفحه با فرمت pdf |
| نوع مقاله | ISI |
| نوع ارائه مقاله | ژورنال |
| رشته های مرتبط با این مقاله | مهندسی کامپیوتر |
| گرایش های مرتبط با این مقاله | مهندسی نرم افزار، مهندسی الگوریتم ها و محاسبات |
| کلمات کلیدی | کد MDS، ماتریس بسیار معین، n کمان کامل |
| کلمات کلیدی انگلیسی | MDS code – superregular matrix – complete n-arc |
| ارائه شده از دانشگاه | مؤسسه تحقیقاتی کامپیوتر و اتوماسیون آکادمی علوم مجارستان |
| بیس | نیست ☓ |
| مدل مفهومی | ندارد ☓ |
| پرسشنامه | ندارد ☓ |
| متغیر | ندارد ☓ |
| فرضیه | ندارد ☓ |
| رفرنس | دارای رفرنس در داخل متن و انتهای مقاله ✓ |
| کد محصول | 12204 |
| نشریه | Citeseerx |
| مشخصات و وضعیت ترجمه فارسی این مقاله | |
| فرمت ترجمه مقاله | pdf و ورد تایپ شده با قابلیت ویرایش |
| وضعیت ترجمه | انجام شده و آماده دانلود |
| کیفیت ترجمه | ویژه – طلایی ⭐️⭐️⭐️ |
| تعداد صفحات ترجمه تایپ شده با فرمت ورد با قابلیت ویرایش | 22 (1 صفحه رفرنس انگلیسی) صفحه با فونت 14 B Nazanin |
| ترجمه عناوین تصاویر و جداول | ترجمه شده است ✓ |
| ترجمه متون داخل تصاویر | ندارد ☓ |
| ترجمه متون داخل جداول | متن برای ترجمه وجود ندارد ✓ |
| ترجمه ضمیمه | ندارد ☓ |
| ترجمه پاورقی | ندارد ☓ |
| درج تصاویر در فایل ترجمه | ندارد ☓ |
| درج جداول در فایل ترجمه | درج شده است ✓ |
| درج فرمولها و محاسبات در فایل ترجمه | به صورت عکس درج شده است ✓ |
| منابع داخل متن | ندارد ☓ |
| منابع انتهای متن | به صورت انگلیسی درج شده است ✓ |
| فهرست مطالب |
|
چکیده مقدمه 1- تعدادی از کدهای MDS دو و سهبعدی غیرمعادل 2- تعدادی از کدهای MDS کامل سهبعدی غیرمعادل 3- دربارهی تعداد کمانها در بیضیها و ابربیضیها 4- تعدادی از ماتریسها حاوی رشتههای فرعی غیرصفر 5- مثالها 6- جدولها منابع |
| بخشی از ترجمه |
|
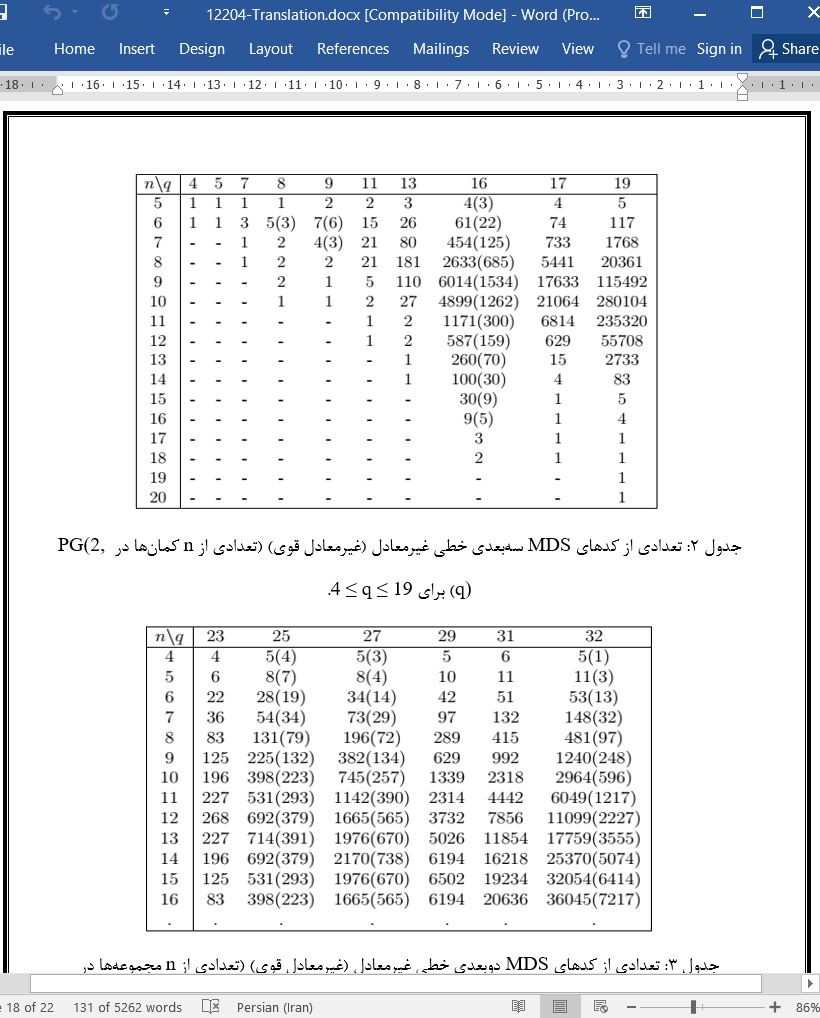
چکیده تعدادی از الف) کدهای MDS دو و سهبعدی غیرمعادل، ب) کدهای MDS کامل سهبعدی غیرمعادل، ج) کدهای MDS سهبعدی که میتوانند بهوسیلهی کمانهای کلاسیک در PG(2, q) توصیف شوند، د) کمانها در حالت منظم ابربیضیشکل و ه) ماتریسهای بسیار معین 2 × n و 3 × n بر روی GF(q) که برای q ≤ 19 و برای تعدادی از حالتها وقتیکه 23 ≤ q ≤ 32 میباشد، ایجاد شدهاند. دستههای معادل هم بر روی PGL(k, q) و هم بر روی PΓL(k, q) در هنگام محاسبات در نظر گرفته شدهاند. اگرچه بیشتر نتایج با کمک یک کامپیوتر بهدست آمده است، اما بعضی از روابط نظری کلی نیز بهصورت فرمول در آمده است. نتایج محاسباتی این پژوهش برای n کمان در PG(2, 31) برای 23 ≤ n ≤ 30 کامل نمیباشد، در نتیجه تخمین اصلی برای کدهای MDS برای کمانهای فضایی تصویری محدود تا حدود 12 بعد از درجهی 31 یعنی برای کدهای MDS تا حدود 13 بعد بر روی GF(31) درست میباشد.
مقدمه هدف پژوهش حاضر، تعیین تعداد دستههای معادل با توجه به سه رابطهی همارزی مختلف و ایجاد پایگاه داده برای کدهای MDS دارای k بعد بر روی میدانهای متناهی GF(q) میباشد که این میدانها شامل یک نماینده از هر دستهی معادل میباشند. در اولین مرحلهی این پروژه، ما محدودیتهایی را برای محدودهی این تخمینها در k ≤ 3 و q ≤ 32 استخراج مینماییم. زمانیکه q بهسمت 32 متمایل میشود، پایگاه داده بسیار بزرگ میگردد و هدف ایجاد دستهبندی بدون استفاده از یک کامپیوتر امکانپذیر نمیباشد. با فراهم کردن جستجوی کامل کامپیوتر، تا زمانیکه q ≤ 32 و q ≤ 19 باشد، مسئله بهصورت کامل بهترتیب برای کدهای MDS دوبعدی و کدهای MDS سهبعدی حل میشود و وقتیکه 23 ≤ q ≤ 32 باشد، کدهای MDS سهبعدی بهصورت جزئی حل میشوند. |
| بخشی از مقاله انگلیسی |
|
Abstract The number of (a) non-equivalent 2 and 3 dimensional MDS codes, (b) non-equivalent 3 dimensional complete MDS codes, (c) 3 dimensional MDS codes that can be described by classical arcs in PG(2, q), (d) arcs in regular hyperovals, and (e) 2 × n and 3 × n superregular matrices over GF(q) are established for q ≤ 19 and for a number of cases when 23 ≤ q ≤ 32. The equivalence classes over both PGL(k, q) and PΓL(k, q) are considered during the computations. Though, most of the results are reached by the help of a computer, also some general theoretical relations are formulated. A computational result of the paper is that there is no complete n-arc in PG(2, 31) for 23 ≤ n ≤ 30 and, consequently, the Main Conjecture for MDS Codes is true for arcs in up to 12 dimensional finite projective spaces of order 31, i.e., for MDS codes of up to 13 dimensions over GF(31).
Introduction The aim of the present work is to determine the number of equivalence classes regarding three different equivalence relations and to build databases of k dimensional MDS codes over the finite fields GF(q) which contain one representant from each equivalence class. In the first phase of the project, we draw the limits for the range of these examinations at k ≤ 3 and q ≤ 32. As the databases become very huge when q advances towards 32, the aimed classification is impossible to carry out without using a computer. By performing exhaustive computer search, the problem is solved completely for 2 dimensional MDS codes until q ≤ 32 and for 3 dimensional MDS codes until q ≤ 19, it is solved partially for 3-dimensional MDS codes when 23 ≤ q ≤ 32. |
|
تصویری از مقاله ترجمه و تایپ شده در نرم افزار ورد |
|
|
| دانلود رایگان مقاله انگلیسی + خرید ترجمه فارسی | |
| عنوان فارسی مقاله: |
دستهبندی کدهای MDS دو و سهبعدی برای 4 ≤ q ≤ 32 |
| عنوان انگلیسی مقاله: |
Classification of 2 and 3 dimensional MDS codes for 4 ≤ q ≤ 32 |
|
|
|