دانلود ترجمه مقاله مدل نظریه صف مورد استفاده برای حل مسئله صف در بانکها 2013 (ترجمه ویژه – طلایی ⭐️⭐️⭐️)

مدل نظریه صف مورد استفاده برای حل مسئله صف در بانکها مطالعه‌ای در مورد بانک اسلامی بنگلادش با مسئولیت محدود، شعبه چاوک بازار ، چیتاگونگ

Queuing Theory Model Used To Solve The Waiting Line Of A Bank -A Study On Islami Bank Bangladesh Limited, Chawkbazar Branch, Chittagong

چکیده
مقدمه
ویژگیهای یک سیستم صف بندی:
ویژگیهای ورود
اندازه جمعیت فراخوانده شده
الگوهای ورودی به سیستم
طرز ورود
ویژگیهای صف انتظار
صف
نظم صف
ویژگیهای مرکز خدمات
ترتیب اصلی سیستم صف بندی
توزیع زمان خدمات رسانی
مدل‌های ریاضی
فرضیات مدل
معادلات صف بندی
معادلات صف بندی موارد زیر را دنبال می‌کنند
مدل صف بندی چند کاناله با ورودیهای پواسون و زمان سرویس دهی نمایی (M/M/S)
برخی روابط مشخصه عملیات کلی
کاربرد مدیریتی نظریه صف
مزایا و محدودیتهای نظریه صف
محدودیت‌های مهم نظریه صف عبارتند از:
کاربرد شکلهای سیستم صف بندی و بحث در مورد هزینه مشتریان برای ایستادن در صف: مطالعه‌ای در مورد بانک اسلامی بنگلادش با مسئولیت محدود، شعبه چاوک بازار ، چیتاگونگ
مجموع هزینه‌های مورد انتظار
تابع هدف
هزینه زمان ایستادن در صف (WC)
نتایج تجربی
نتیجه گیری
منابع

چکیده

سیستم‌های خدماتی و صفوف انتظار، بخشهای مهمی از دنیای کسب و کار هستند. ما در این مقاله، چندین موقعیت معمول صف بندی را توضیح داده و مدلهای ریاضی را برای تحلیل صفوف انتظار، ذیل فرضیات خاصی  ارائه می‌دهیم. این فرضیات عبارتند از: (1) افراد از یک جمعیت نامحدود یا بسیار بزرگ وارد می شوند، (2) ورودی‌ها دارای توزیع پواسون هستند، (3) ورودی‌ها بر مبنای FIFO مورد پردازش قرار می‌گیرند و روگردانی یا امتناع نمی‌کنند، (4) زمان خدمات رسانی از یک توزیع نمایی منفی پیروی می‌کند و یا ثابت است، و (5) نرخ متوسط خدمات سریعتر از نرخ متوسط ورود است.

مدلی که در این بانک برای مشتریان در سطحی از خدمات نشان داده شده، یک مدل صف بندی چند کاناله با ورودی پواسون و زمان سرویس دهی نمایی (M/M/S) است. پس از اینکه یک سری از ویژگیهای عملیاتی محاسبه شد، کل هزینه‌های مورد انتظار مورد بررسی قرار می‌گیرند. کل هزینه‌ها مجموع هزینه‌های ارائه خدمات به علاوۀ هزینه زمان ایستادن در صف است. در نهایت، میزان کل حداقل هزینه مورد انتظار را مشخص می‌کنیم.

مقدمه

نظریه صف از کار تحقیقاتی یک مهندس دانمارکی به نام A.K. Erlang منشاء گرفته است. در سال 1909، Erland میزان متغیر تقاضا در ترافیک تلفنی را مورد بررسی قرار داد. هشت سال بعد، او گزارشی را منتشر کرد که در آن تأخیر در تجهیزات شماره گیری خودکار را مورد نظر قرار داده بود. در پایان جنگ جهانی دوم، کارهای اولیه Erlang به مسائل کلی‌تر و برنامه نویسی کسب و کار از صفوف انتظار تعمیم داده شد.

ABSTRACT

Waiting lines and service systems are important parts of the business world. In this article we describe several common queuing situations and present mathematical models for analyzing waiting lines following certain assumptions. Those assumptions are that: (1) arrivals come from an infinite or very large population, (2) arrivals are Poisson distributed, (3) arrivals are treated on a FIFO basis and do not balk or renege, (4) service times follow the negative exponential distribution or are constant, and (5) the average service rate is faster than the average arrival rate.

The model illustrated in this Bank for customers on a level with service is the multiple-channel queuing model with Poisson Arrival and Exponential Service Times (M/M/S). After a series of operating characteristics are computed, total expected costs are studied, total costs is the sum of the cost of providing service plus the cost of waiting time. Finally we find the total minimum expected cost.

INTRODUCTION

Queuing theory had its beginning in the research work of a Danish engineer named A.K. Erlang. In 1909 Erland experimented with fluctuating demand in telephone traffic. Eight years letter he published a report addressing the delays in automatic dialing equipment. At the end of World War II, Erlang’s early work was extended to more general problems and to business applications of waiting lines.

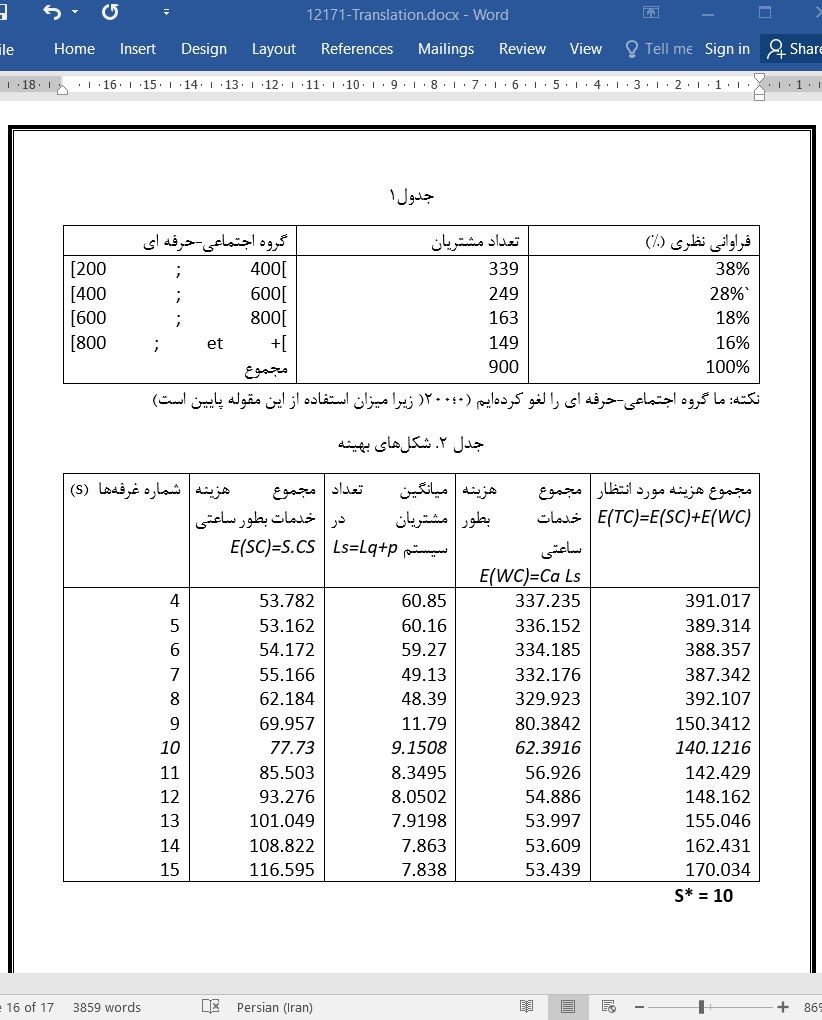
تصویری از مقاله ترجمه و تایپ شده در نرم افزار ورد

مدل نظریه صف مورد استفاده برای حل مسئله صف در بانکها مطالعه‌ای در مورد بانک اسلامی بنگلادش با مسئولیت محدود، شعبه چاوک بازار ، چیتاگونگ

Queuing Theory Model Used To Solve The Waiting Line Of A Bank -A Study On Islami Bank Bangladesh Limited, Chawkbazar Branch, Chittagong