این مقاله انگلیسی ISI در نشریه ساینس دایرکت (الزویر) در 15 صفحه در سال 2018 منتشر شده و ترجمه آن 46 صفحه میباشد. کیفیت ترجمه این مقاله ویژه – طلایی ⭐️⭐️⭐️ بوده و به صورت کامل ترجمه شده است.
| دانلود رایگان مقاله انگلیسی + خرید ترجمه فارسی | |
| عنوان فارسی مقاله: |
متدهای راه حل برای مساله بهینه سازی سینی |
| عنوان انگلیسی مقاله: |
Solution methods for the tray optimization problem |
|
|
|
| مشخصات مقاله انگلیسی (PDF) | |
| سال انتشار | 2018 |
| تعداد صفحات مقاله انگلیسی | 15 صفحه با فرمت pdf |
| نوع مقاله | ISI |
| نوع نگارش | مقاله پژوهشی (Research Article) |
| نوع ارائه مقاله | ژورنال |
| رشته های مرتبط با این مقاله | مهندسی صنایع |
| گرایش های مرتبط با این مقاله | برنامه ریزی و تحلیل سیستم ها، بهینه سازی سیستم ها |
| چاپ شده در مجله (ژورنال) | مجله اروپایی تحقیقات عملیاتی – European Journal of Operational Research |
| کلمات کلیدی | برنامه ریزی خطی صحیح، OR در خدمات سلامتی، موجودی استریل شده، تولید سطر و ستون و اکتشافی |
| کلمات کلیدی انگلیسی | OR in Health Services – Sterile Inventory – Integer Linear Programming – Row and Column Generation – Heuristics |
| ارائه شده از دانشگاه | دانشکده اقتصاد اراسموس ، دانشگاه اراسموس روتردام هلند |
| نمایه (index) | Scopus – Master journals – JCR |
| نویسندگان | Twan Dollevoet، J. Theresia van Essen، Kristiaan M. Glorie |
| شناسه شاپا یا ISSN | ISSN 0377-2217 |
| شناسه دیجیتال – doi | https://doi.org/10.1016/j.ejor.2018.05.051 |
| ایمپکت فاکتور(IF) مجله | 4.712 در سال 2018 |
| شاخص H_index مجله | 226 در سال 2019 |
| شاخص SJR مجله | 2.205 در سال 2018 |
| شاخص Q یا Quartile (چارک) | Q1 در سال 2018 |
| بیس | نیست ☓ |
| مدل مفهومی | ندارد ☓ |
| پرسشنامه | ندارد ☓ |
| متغیر | دارد ✓ |
| رفرنس | دارای رفرنس در داخل متن و انتهای مقاله ✓ |
| کد محصول | 10074 |
| لینک مقاله در سایت مرجع | لینک این مقاله در نشریه Elsevier |
| نشریه الزویر |  |
| مشخصات و وضعیت ترجمه فارسی این مقاله (Word) | |
| وضعیت ترجمه | انجام شده و آماده دانلود در فایل ورد و PDF |
| کیفیت ترجمه | ویژه – طلایی ⭐️⭐️⭐️ |
| تعداد صفحات ترجمه تایپ شده با فرمت ورد با قابلیت ویرایش | 46 صفحه با فونت 14 B Nazanin |
| ترجمه عناوین تصاویر و جداول | ترجمه شده است ✓ |
| ترجمه متون داخل تصاویر | ترجمه نشده است ☓ |
| ترجمه متون داخل جداول | ترجمه نشده است ☓ |
| ترجمه ضمیمه | ترجمه شده است ✓ |
| درج تصاویر در فایل ترجمه | درج شده است ✓ |
| درج جداول در فایل ترجمه | درج شده است ✓ |
| درج فرمولها و محاسبات در فایل ترجمه | به صورت عکس درج شده است ✓ |
| منابع داخل متن | به صورت انگلیسی درج شده است ✓ |
| منابع انتهای متن | به صورت انگلیسی درج شده است ✓ |
| فهرست مطالب |
|
چکیده 1. مقدمه 2- بیان مساله 2-1- محدودیت های ظرفیت 2-2- تابع هدف 3- روش راه حل 3-1- روش راه حل دقیق 3-2- روش های راه حل اکتشافی تابع تناسب تکثیر (تولید مثل) 4- طراحی شبیه سازی 4-1- داده ها 4-2- تولید نمونه 4-3- شبیه سازی دینامیکی 5- نتایج محاسباتی 5-1- ارزیابی عملکرد بر اساس نمونه های تولید شده تصادفی 5-2- ارزیابی عملکرد در یک بازه زمانی طولانی تر 6- نتیجه گیری ها و پیشنهادات پوست A : مجموعه ها، پارامترها و متغیرها مجموعه ها پارامترها متغیرها پیوست B: تولید سطر و ستون: اثبات ها و مشتق ها پیوست C مساله اختصاص سینی، NP-hard است منابع |
| بخشی از ترجمه |
|
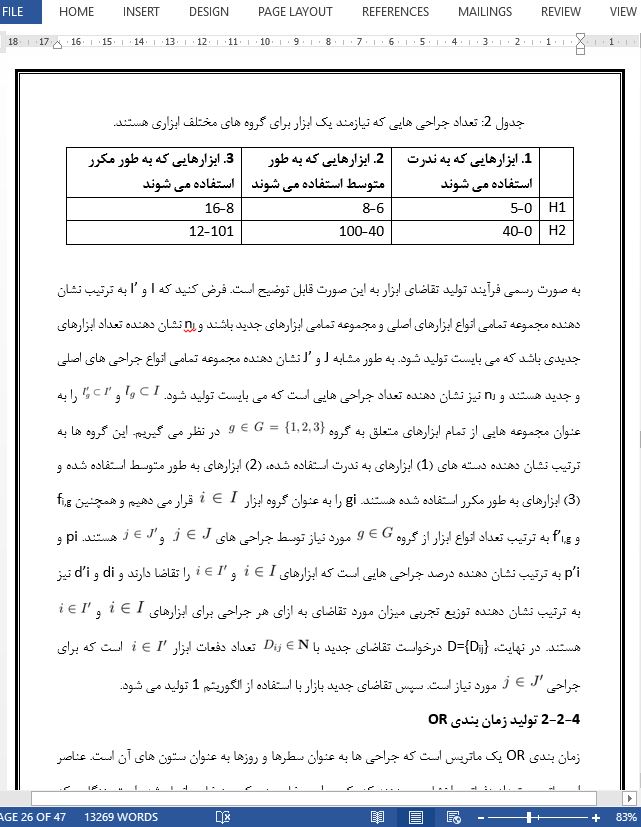
چکیده بیمارستان ها معمولاً به منظور انجام جراحی های پزشکی فهرست بزرگی از ابزارهای جراحی را نگهداری می کنند. این ابزارها می بایست پیش از انجام هر جراحی استریلیزه شوند. به طور معمول این ابزارها در سینی های مخصوصی نگهداری می شوند. برای یک جراحی ممکن است از سینی های متعددی استفاده شود در حالی که یک سینی ممکن است حاوی ابزارهایی باشد که برای چندین مرحله جراحی مورد نیاز باشد. مساله بهینه سازی سینی (TOP) شامل سه مرحله تصمیم گیری اصلی است: (1) اختصاص ابزارها به سینی ها، (2) اختصاص سینی ها به جراحی ها و (3) تعداد سینی هایی که می بایست در فهرست ابزارها نگهداری شود. تصمیمات مربوط به مساله TOP می بایست به نحوی اتخاذ شوند که کل هزینه های عملیاتی به حداقل برسند و به نحوی باشد که ابزارهای کافی برای هر جراحی به مقدار کافی در دسترس وجود داشته باشد. این مقاله روش های حل دقیق و اکتشافی را برای مساله TOP ارائه می کند و مورد ارزیابی قرار می دهد. ما روش های مختلف حل را براساس زمان محاسبات و کیفیت راه حل مورد مقایسه قرار می دهیم. علاوه بر این، روش های جدیدی که ارائه می شوند، اولین روش هایی هستند که قابلیت حل نمونه ها در اندازه واقعی را دارند. متقاعدکننده ترین روش شامل یک الگوریتم حریصانه پیشرفته با مقیاس پذیری بالا است. نتایج به دست آمده نشان می دهند که نتایج حاصل از این روش به طور متوسط به نتایج حاصل از دیگر روش های بررسی شده بسیار نزدیک است، در حالی که می تواند به سادگی توسط بیمارستان های بزرگ به کار گرفته شود. یافته های به دست آمده با توجه به نوسانات در زمان بندی های بلند مدت OR مقاوم هستند.
6- نتیجه گیری ها و پیشنهادات در این مقاله روش های متعدد راه حل برای مساله بهینه سازی سینی جراحی (TOP) پیشنهاد داده شده است. در مساله TOP، ترکیب سینی های ابزار، اختصاص این سینی ها به جراحی ها و دستیابی به تعداد سینی ها از یک نوع به طور همزمان تعیین می شوند. به طور ویژه ما فرمول دقیقی از ILP، روش تولید سطر و ستون، روش اکتشاف حریصانه و برخی روش های فرا اکتشافی را در نظر گرفته ایم. ما در یک مطالعه به شدت محاسباتی این روش های راه حل را براساس نمونه های متعددی که از واقعیت الهام گرفته شده است، با یکدیگر مقایسه کرده ایم. علاوه بر این، ما عملکرد راهکارها را با استفاده از شبیه سازی در یک بازه زمانی طولانی تر مورد آزمایش قرار داده ایم. روش اکتشاف حریصانه انواع متعدد سینی را ایجاد می کند و سپس مدل ILP را برای مساله اختصاص سینی به طور بهینه حل می کند. نتایج محاسباتی ما نشان می دهند که این روش عملکرد خوبی دارد، به ویژه هنگامی که زمان های محاسباتی کوتاه در نظر گرفته می شوند. روش اکتشاف حریصانه راه حل هایی را ارائه می دهد که به طور متوسط 7 درصد بدتر از بهترین راه حل های یافت شده هستند. |
| بخشی از مقاله انگلیسی |
|
Abstract In order to perform medical surgeries, hospitals keep large inventories of surgical instruments. These instruments need to be sterilized before each surgery. Typically the instruments are kept in trays. Multiple trays may be required for a single surgery, while a single tray may contain instruments that are required for multiple surgical procedures. The tray optimization problem (TOP) consists of three main decisions: (i) the assignment of instruments to trays, (ii) the assignment of trays to surgeries, and (iii) the number of trays to keep in inventory. The TOP decisions have to be made such that total operating costs are minimized and such that for every surgery sufficient instruments are available. This paper presents and evaluates several exact and heuristic solution methods for the TOP. We compare solution methods on computation time and solution quality. Moreover, we conduct simulations to evaluate the performance of the solutions in the long run. The novel methods that are provided are the first methods that are capable of solving instances of realistic size. The most promising method consists of a highly scalable advanced greedy algorithm. Our results indicate that the outcomes of this method are, on average, very close to the outcomes of the other methods investigated, while it may be easily applied by (large) hospitals. The findings are robust with respect to fluctuations in long term OR schedules.
6- Conclusions and recommendations In this paper, we have developed several solution methods for the tray optimization problem (TOP). In the TOP, one simultaneously determines the composition of instrument trays, the assignment of these trays to surgeries, and the number of trays of a certain type to acquire. In particular, we have considered an exact ILP formulation, a row & column generation approach, a greedy heuristic, and some metaheuristics. In an extensive computational study, we have compared these solution methods on several instances that are inspired by practice. Furthermore, we have tested the performance of the solutions on a longer time horizon using simulation. The greedy heuristic constructs several tray types and then solves the ILP model for the tray assignment problem optimally. Our computational results indicate that this method performs surprisingly well, especially considering the short computation times. The greedy heuristic gives solutions that are on average roughly 7% worse than the best solutions we found. |
|
تصویری از مقاله ترجمه و تایپ شده در نرم افزار ورد |
|
|
| دانلود رایگان مقاله انگلیسی + خرید ترجمه فارسی | |
| عنوان فارسی مقاله: |
متدهای راه حل برای مساله بهینه سازی سینی |
| عنوان انگلیسی مقاله: |
Solution methods for the tray optimization problem |
|
|
|