| دانلود رایگان مقاله انگلیسی + خرید ترجمه فارسی
|
|
| عنوان فارسی مقاله: |
روش و مدل عددی جدید برای ضربه آبی (قوچ) |
| عنوان انگلیسی مقاله: |
New Numerical Model And Technique For Waterhammer |
|
|
| مشخصات مقاله انگلیسی (PDF) | |
| سال انتشار | 1984 |
| تعداد صفحات مقاله انگلیسی | 13 صفحه با فرمت pdf |
| رشته های مرتبط با این مقاله | ریاضی و مهندسی مکانیک |
| گرایش های مرتبط با این مقاله | مکانیک سیالات، ریاضی کاربردی و تحقیق در عملیات |
| مجله | مجله مهندسی هیدرولیک – Journal of Hydraulic Engineering |
| دانشگاه | تحقیقات مهندسی، گروه مهندسی هیدرولیک، نهاد ملی تحقیقات، مهندسی کشاورزی، ژاپن |
| رفرنس | دارد |
| لینک مقاله در سایت مرجع | لینک این مقاله در سایت ASCE |
| نشریه ASCE | |
| مشخصات و وضعیت ترجمه فارسی این مقاله (Word) | |
| تعداد صفحات ترجمه تایپ شده با فرمت ورد با قابلیت ویرایش و فونت 14 B Nazanin | 20 صفحه |
| ترجمه عناوین تصاویر و جداول | ترجمه شده است |
| ترجمه متون داخل تصاویر | ترجمه شده است |
| ترجمه متون داخل جداول | ترجمه شده است |
| ترجمه ضمیمه | ترجمه شده است |
| درج تصاویر در فایل ترجمه | درج شده است |
| درج جداول در فایل ترجمه | درج شده است |
| درج فرمولها و محاسبات در فایل ترجمه به صورت عکس | درج شده است |
فهرست مطالب:
چکیده
مقدمه
معادلات پایه
معادلات تفاضل محدود
روش نیوتن – رافسون
خطای کوتاه سازی.
روش صریح جدید
محاسبه ی جریان یکنواخت
رابطه ی جدید روش نیوتن – رافسون
نتایج عددی
خلاصه و نتایج
پیوست.- توضیح نمادها
بخشی از ترجمه:
خلاصه و نتایج
در این تحقیق میزان کارایی مدل مرتبه دوم برای معادلات ساده شده ی حاکم بر ضربه ی آبی ایجاد شده در سیستمهای لوله کشی مورد آنالیز قرار گرفته است. در این مطالعه نویسندگان روشهای تحلیلی سری و نیوتن – رافسون جدیدی را ارائه نموده اند که در آنها ترمهای کم اهمیت حذف شده اند که البته خطای کوتاه سازی ناشی از حذف این ترمها محاسبه و در نظر گرفته شده است.
با انجام محاسباتی کمتر نسبت به آنچه که قبلا مورد نیاز بود، روشهای جدید می توانند تحلیلی را با دقت مورد نیاز و بدون هیچگونه تکرار ارائه نمایند. پس، در مقایسه با روش ارائه شده توسط مدل مرتبه اول، مدل مرتبه دوم روشهای به مراتب کارا و دقیق تری را می دهد، این روشها نه تنها برای سیستمهای دارای افت اصطکاک زیاد بلکه برای سیستمهایی که افت اصطکاکشان نسبتا زیاد هم باشد می توانند کاربرد داشته باشند. به هر حال، از آنجا که مدل مرتبه دوم در محاسبات جریان یکنواخت با خطا همراه است، روشهایی برای از بین بردن یا کاهش مقدار این خطا نشان داده شده اند. اعتبار آنالیزها توسط محاسبات عددی مورد ارزیابی قرار گرفته اند که در آنها پارامترهای سیستم تغییرات گسترده ای دارند.
بخشی از مقاله انگلیسی:
SUMMARY AND CONCLUSIONS
How efficiently the second-order model is handled is analysed for the simplified equations governing waterhammer appearance in piping systems. The series solution method and the Newton-Raphson method with the new calculation steps are proposed by the writers through omitting trivial terms computed within the truncation error. With fewer calculations than required previously, the new methods can yield a solution with the required accuracy without any iteration. Then, compared with the procedure given by the first-order model, the second-order model offers more efficient and accurate procedures, which are applicable not only to systems with high friction losses but also to systems with moderately high friction losses. However, since the second-order model introduces an error in steady flow calculations, ways to remove or reduce this error are shown. The validity of the analyses is examined by the numerical computations in which the system parameters are varied widely.
|
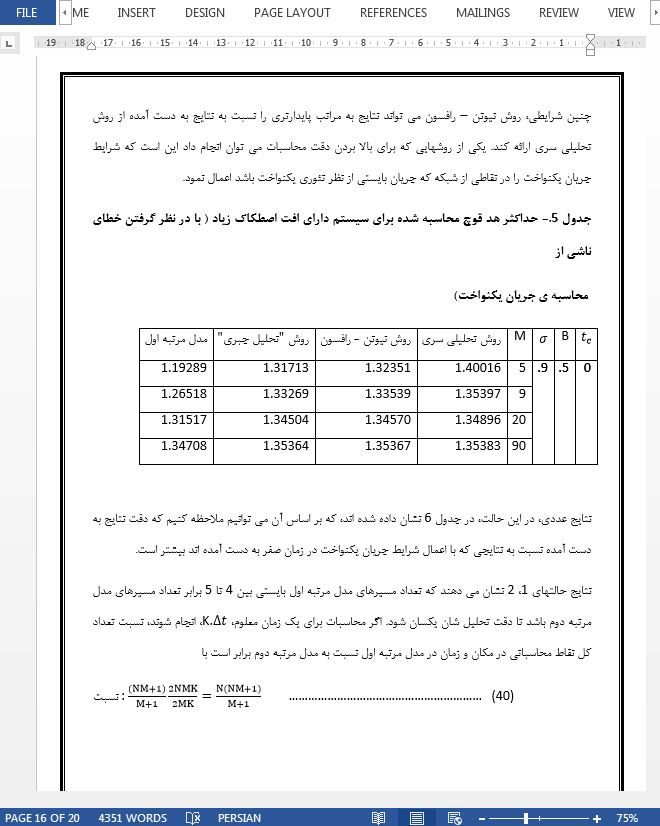
تصویری از مقاله ترجمه و تایپ شده در نرم افزار ورد |
|
|
| دانلود رایگان مقاله انگلیسی + خرید ترجمه فارسی
|
|
| عنوان فارسی مقاله: |
روش و مدل عددی جدید برای ضربه آبی (قوچ) |
| عنوان انگلیسی مقاله: |
New Numerical Model And Technique For Waterhammer |
|
|